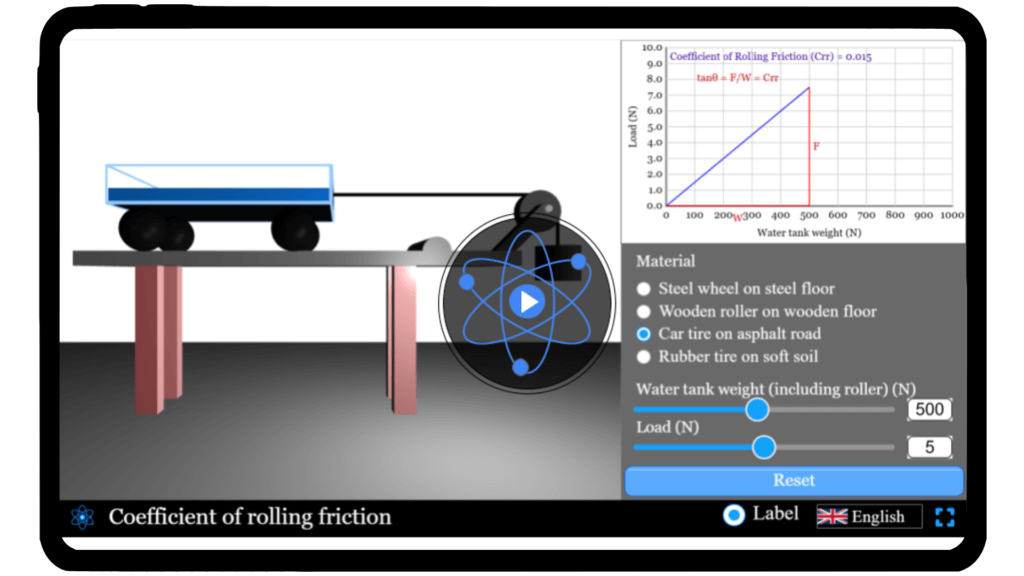
Coefficient of Rolling Friction Simulator
Experiment how different surface types affect rolling friction, and measure the minimum force required to overcome the limiting friction.
Rolling friction
The wheel transformed how people move and transport goods. Even before modern science, it was clear wheels meet less resistance than other shapes; now we can measure that precisely — rolling friction is usually less than other forms of friction. Try our interactive simulator to explore how mass, wheel radius, and surface type affect rolling resistance and deceleration.
\( F_r =\mu_r N \)
Mathematical description
where:
- \( F_r \) is rolling resistance force
- \( \mu_r \) is the coefficient of rolling friction
- \( N \) is the Normal force
FAQs on Rolling friction
Qus 1. What is rolling friction (rolling resistance)?
Rolling friction — often called rolling resistance — is the force that opposes the motion of a wheel or rolling body across a surface. It arises mainly from hysteresis and deformation of the wheel and the surface, converting useful kinetic energy into heat.
Qus 2. What causes rolling resistance?
The dominant causes are material deformation (hysteresis) in tires/wheels, permanent surface deformation, micro-slip in the contact patch, and bearing or structural losses; together these dissipate energy each wheel rotation. Understanding these components helps explain why soft tires and soft surfaces increase resistance.
Qus 3. What are typical values of the coefficient of rolling resistance
Typical coefficient of rolling friction values depend on material: steel-on-steel rails can be below 0.001, passenger-car tires ~0.01–0.02, and bicycle tires range 0.002–0.005 depending on type and pressure. Exact values vary with speed, pressure, load and temperature.
Qus 4. How is rolling friction different from sliding friction?
When two surfaces slide, those tiny peaks continually catch, shear, and break as one surface moves over the other — that persistent scraping is where most energy is lost. In rolling, the contact patch doesn’t continuously scrape across the surface; instead the wheel and the road flex and recover as the contact region moves, so the main loss comes from repeated bending and a little bit of local slipping, not from constant tearing. That difference makes rolling resistance much smaller than sliding friction for similar materials.
Qus 5. Does rolling resistance depend on speed?
Rolling resistance usually increases with speed because a rolling tire deforms and recovers more times per second as it goes faster. Those repeated deformations, internal tread motion, and small air-pumping effects convert more mechanical energy into heat, raising the effective coefficient of rolling resistance. The change is modest at normal road speeds but becomes more pronounced at higher speeds and under heavy loads.
Qus 6. Does the wheel's radius have any effect on the rolling resistance?
Yes, larger wheels experience less rolling resistance than smaller ones, which is why they roll more smoothly. For example, bicycles with big wheels travel more efficiently than hand carts that use small caster wheels.
Qus 7. Why do wheel's with more radius face less rolling resistance?
In an ideal scenario, when a perfectly rigid wheel rolls, the contact point between the wheel and surface is a simple “point”.
But in reality, wheels and surfaces squash slightly where they touch (rubber tire, carpet, wood floor, etc.) causing a “flattening”.
This flattening creates a contact patch and the contact is no more a point.
Now lets look at the contact patch- as the wheel moves forward the front edge of is being loaded (new material is being squashed) and back edge is recovering (material springs back).
Because the recovery is not perfectly elastic, the pressure at the front of the patch is slightly greater than at the back.
This imbalance shifts the resultant normal force (N) (wheel weight) a small distance ahead of the wheel’s center line.
That forward shift is the resistance arm b, which is equal to the length of the contact patch
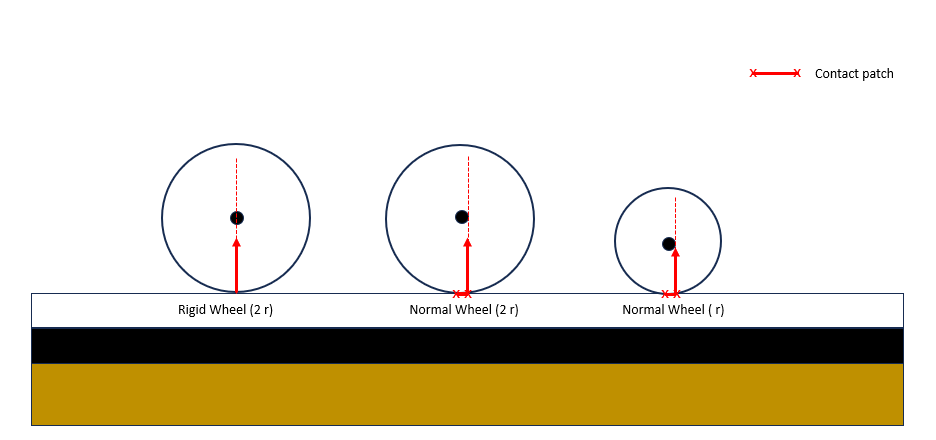
Now as seen in the above image, for perfectly rigid wheels \( b=0 \) and for non-rigid wheels \(b \neq 0\) hence the contact patch produces a torque resisting rotation \( \tau= N. b\). The resisting torque can be thought of coming from rolling friction, which acts at the opposite direction of wheel’s motion.
\[
\tau =R. F_r
\]
\[
N. b =R. F_r
\]
\[
F_r = \frac{N. b}{R}
\]
\[
\mu_r N= \frac{N. b}{R}
\]
\[
\mu_r = \frac{ b}{R}
\]
Hence the coefficient of rolling friction depends upon the radius of the wheel. As the wheel’s radius increases, the rolling friction resistance decreases.