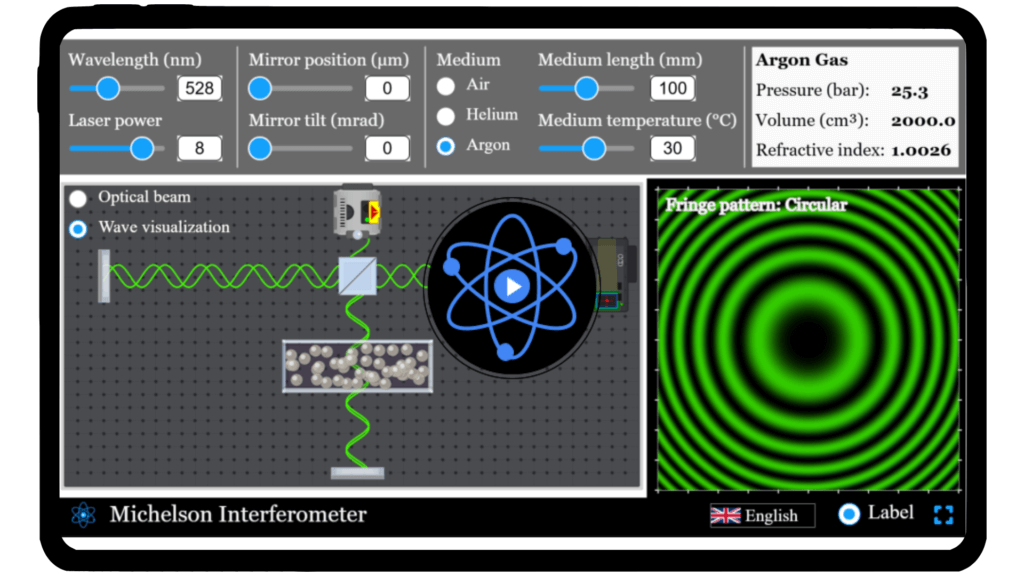
Michelson interferometer Simulator
Experiment with the Michelson Interferometer to explore light interference. Adjust mirror positions and wavelengths to observe dynamic fringe patterns and understand precision measurement in optics.
Michelson interferometer
From measuring tiny distances to detecting gravitational waves, the Michelson Interferometer is a masterpiece of optical physics. At its core lies the elegant principle of light interference — where even the smallest change in distance can shift entire patterns of light. Ever wondered how scientists detect the invisible? With our interactive simulator, you can explore this precision instrument hands-on. Move mirrors, adjust wavelengths, and watch interference fringes respond in real time. Discover the science that helped reshape modern physics — start experimenting with the Michelson Interferometer today!
\( \Delta x = \frac{m \lambda}{2} \)
Mathematical description
This is the Michelson Fringe shift formula where:
- \( \Delta x \) is the change in mirror position
- \(m \) is the number of fringes shifted (bright or dark)
- \( \lambda \) is the wavelength of light used
FAQs on Michelson interferometer
Qus 1. What is a Michelson interferometer?
The Michelson Interferometer is a precise optical instrument that splits a single light beam into two separate paths using a partially reflective mirror. These beams reflect back and recombine, creating an interference pattern. This pattern helps detect extremely small changes in distance or optical path length with high accuracy.
Qus 2. How does a Michelson interferometer work?
It works by dividing a beam of light into two beams traveling different paths. One beam reflects off a fixed mirror, while the other bounces off a movable mirror. When the two beams meet again, they create an interference pattern of bright and dark fringes. Shifts in these fringes correspond to tiny changes in the mirror’s position or path length.
Fringe shift Formula:
\begin{equation}
\Delta x = \frac{m \lambda}{2}
\end{equation}
where:
- \( \Delta x \) is the change in mirror position
- \(m \) is the number of fringes shifted (bright or dark)
- \( \lambda \) is the wavelength of light used
Qus 3. What can you measure with a Michelson interferometer?
This device can measure various physical quantities with high precision, including:
- Wavelength of light,
Refractive index of materials,
Micrometer-scale displacements,
And even gravitational waves (e.g., LIGO)
Qus 4. Why is a laser or monochromatic light source used in the Michelson interferometer experiment?
Using monochromatic (single wavelength) and coherent light, like that from a laser, ensures the interference fringes are sharp and well-defined. Lasers have a long coherence length, meaning the light waves remain in phase over longer distances, which is essential for producing clear and stable fringe patterns.
Qus 5. How do fringe patterns form?
Fringe patterns arise from the constructive and destructive interference of two light waves. When the path difference between the two beams equals an integer multiple of the light’s wavelength, bright fringes appear (constructive interference). When the path difference is a half-integer multiple, dark fringes form (destructive interference).
Qus 6. What are common sources of error in the Michelson interferometer experiment?
In the Michelson interferometer experiment, accuracy can be affected by:
Vibrations
Air currents
Thermal drift
And optical misalignment.
Proper isolation, environmental control, and careful setup are crucial to minimize these errors.
Qus 7. Can arm lengths be different in an interferometer?
Yes, the arms of the interferometer can have different lengths as long as the difference is within the coherence length of the light source. Coherence length is the length/distance over which the light remains in phase after coming out of the source.
If the path difference is too large, the interference pattern disappears. This flexibility allows applications in spectroscopy and material analysis.
Qus 8. How is the Michelson Interferometer used in astronomy?
Astronomers use a modified version called the stellar interferometer to measure the angular diameters of stars. By combining light from separate telescopes, this technique, pioneered by Michelson, allows extremely precise measurements beyond the resolution of single telescopes.
Qus 9. What is Michelson visibility (fringe visibility)?
Michelson visibility is a measure of how distinct the bright and dark fringes are in the interference pattern. It is calculated by comparing the maximum and minimum light intensities. High visibility means the beams are highly coherent, resulting in sharp, clear fringes.
\begin{equation}\nu = \frac{I_{\max} – I_{\min}}{I_{\max} + I_{\min}}\end{equation}
Qus 10. Why does a Michelson Interferometer need a compensator plate?
A compensator plate balances the optical path lengths by making sure both light beams pass through the same amount of glass in the beam splitter. This equalization improves the visibility and contrast of interference fringes, especially when using white light, which contains multiple wavelengths.
