Refractive index of liquid using convex lens & plane mirror Simulator
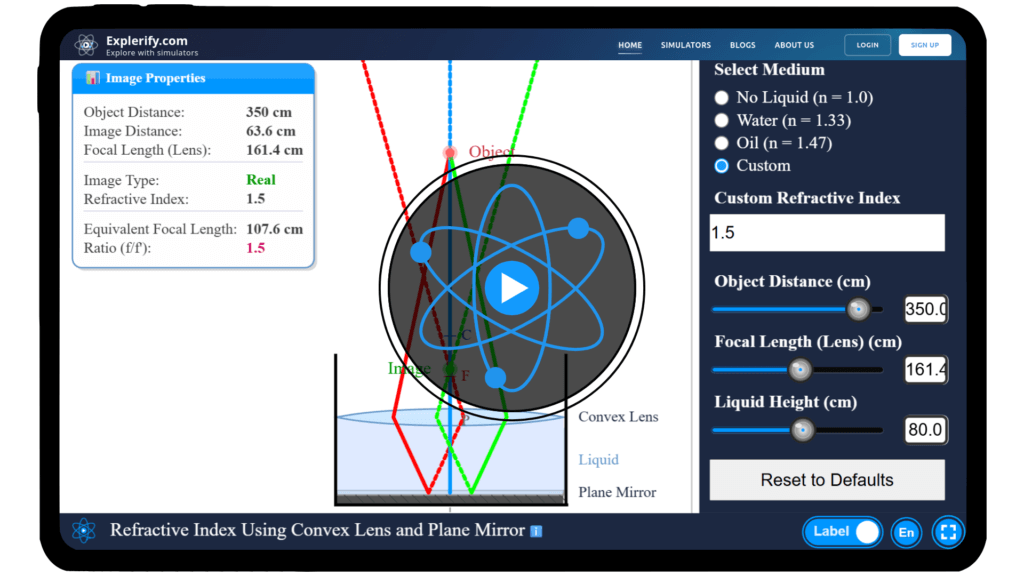
Investigate how the focal length of a convex lens changes with a liquid layer on a plane mirror, and experiment with varying liquid depths and lens parameters using our interactive refractive index simulator.
Refractive index fo liquid using convex lens & plane mirror
Physics shapes our world in subtle yet remarkable ways, often without us realizing it. Have you ever wondered how scientists determine the refractive index of a liquid using just a convex lens and a plane mirror? This seemingly simple setup reveals profound optical principles through the way a lens’s focal length shifts when a thin layer of liquid is introduced. With our interactive simulator, you can explore this phenomenon firsthand. Adjust the liquid depth, vary lens parameters, observe the changing focal point, and uncover the science behind refractive index measurement. Begin your journey into the captivating world of optics — experiment with the refractive index of liquids today!
\( \mu = \frac{f}{f _{eff}}\)
Mathematical description
where:
- \( \mu \) refractive index of the liquid
- \( f \) focal length of the convex lens in air
- \( f_{eff} \) effective focal length of combine system with lens and liquid.
FAQs
Qus 1. What is the principle behind determining the refractive index using a convex lens and plane mirror?
This method is based on measuring the change in the effective focal length of a convex lens when a thin layer of liquid is introduced between the lens and a plane mirror. The liquid alters the lens’s optical power, and the refractive index is calculated using the relationship between the original and modified focal lengths.
Qus 2. How does the presence of a liquid change the focal length of the convex lens?
When a liquid is added, the lower curved surface of the lens effectively becomes a composite interface of glass–liquid–air instead of glass–air. This changes the refraction at that surface, resulting in a different effective focal length.
Qus 3. Who first introduced the method of using a convex lens and plane mirror to measure refractive index?
This technique evolved from classical optical experiments on lens behavior in different media. While not attributed to a single inventor, it stems from 19th-century developments in geometrical optics and refractometry, following the foundational work of scientists like Snell, Fermat, and Newton.
Qus 4. What historical experiments led to this method?
Early studies on the bending of light through different media, the lens-maker’s formula, and methods for measuring focal length paved the way. Researchers began observing how immersion of lenses in liquids modified their properties, eventually leading to practical refractive index determination techniques.
Qus 5. What are the practical applications of this experiment?
This method is widely used to determine the refractive index of:
Transparent liquids
Oils and solvents
Laboratory chemicals
Optical coatings
It helps in fields such as material science, chemical analysis, lens manufacturing, and educational optics labs.
Qus 6. Why is a plane mirror used in this setup?
The plane mirror reflects light back through the lens, creating a sharp image of a distant object at the focal point. This ensures that the focal length can be accurately measured before and after adding the liquid.
Qus 7. What advantages does this method have over other refractometers?
Simple and inexpensive setup
No need for complex instruments
Works well with small quantities of liquid
Demonstrates fundamental optical principles
Great for teaching and conceptual understanding
Qus 8.Can any convex lens be used for this experiment?
A thin convex lens with a known radius of curvature works best. A plano-convex lens is commonly used because its geometry simplifies the analysis and improves measurement precision.
Qus 9. Why does the refractive index increase when the focal length decreases?
Refractive index determines how much light bends in a medium. A liquid with higher refractive index bends light more strongly at the lens–liquid interface, which increases the lens’s converging power and reduces the effective focal length.
Qus 10. What role does lens curvature play in this experiment?
The radius of curvature directly affects the focal length. Accurate measurement or knowledge of the curvature helps in understanding how the liquid layer influences refraction at the curved surface.