Young's Modulus Simulator
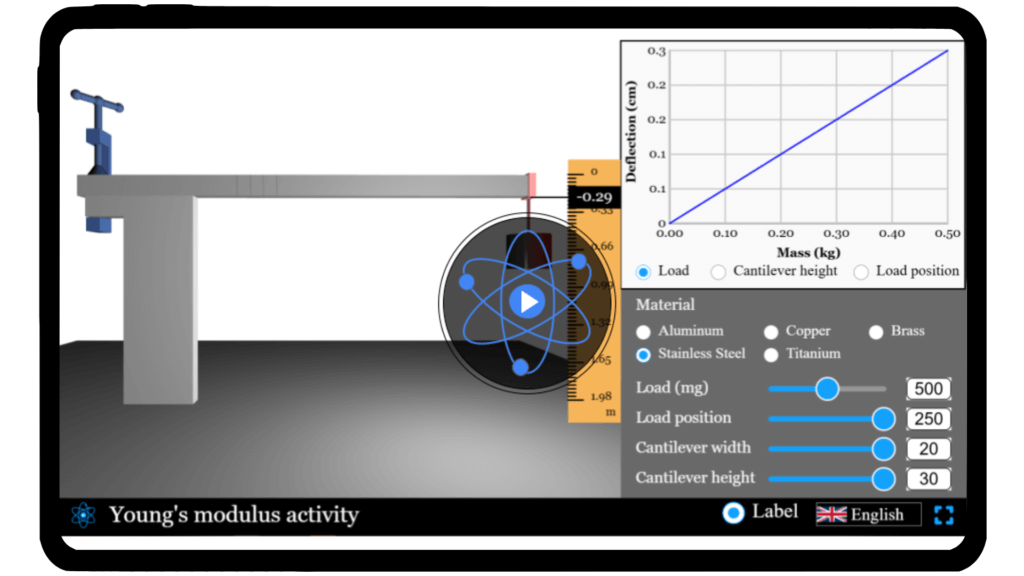
Investigate material deformation and experiment with varying beam dimensions, applied forces, and materials to observe deflection using our interactive simulator.
Young's Modulus
Physics is all around us, shaping the way materials behave under forces in everyday life. Have you ever wondered why a beam bends when a weight is applied? This bending, or deflection, is governed by the material’s Young’s Modulus, a fundamental property that measures stiffness. With our interactive simulator, you can explore this concept firsthand. Adjust beam dimensions, material type, and applied forces, then observe how the deflection changes. Discover the science behind material deformation and deepen your understanding of mechanics — experiment with Young’s Modulus today!
\( \delta = \frac{m g \, x^2 (3L – x)}{2 E b h^3} \)
Mathematical description
where:
- \( m \) mass of load
- \( g \) acceleration due to gravity
- \( x \)position of load from the fixed end
- \( L \) length of the beam
- \( E \) Young’s Modulus
- \( b \) width of the beam
- \( h \) height of the beam
FAQs on Young's modulus
Qus 1. What is Young’s Modulus?
Young’s Modulus is a measure of a material’s stiffness. It quantifies how much a material will stretch or compress under a given force.
Qus 2. Why is Young’s Modulus important?
It helps engineers and scientists choose materials for structures, ensuring they can withstand forces without bending or breaking excessively.
Qus 3. How does changing the material affect deflection?
Materials with higher Young’s Modulus are stiffer and bend less under the same load, while softer materials bend more.
Qus 4. What is the effect of beam dimensions on deflection?
Taller and wider beams are stiffer and deflect less. Longer beams bend more easily under the same load.
Qus 5. How accurate is this simulation compared to real experiments?
The simulator is ideal for learning and visualization. It approximates real-world behavior but assumes ideal conditions (uniform material, perfect beam, no friction).