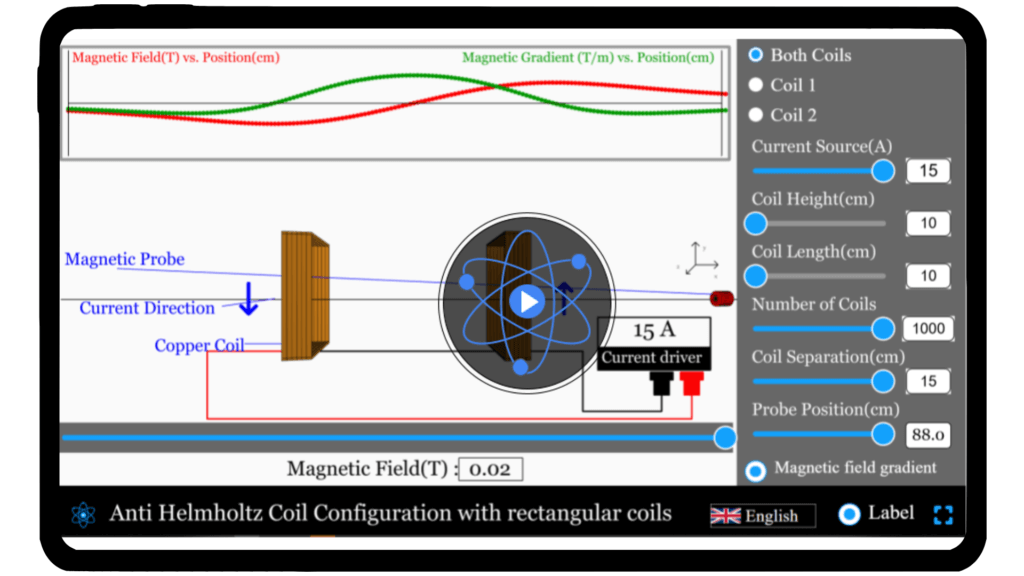
Anti Helmholtz configuration with rectangular coils
Visualize and experiment with the magnetic field at the center of a pair of coils in a Anti-Helmholtz configuration using our interactive simulator.
Anti-Helmholtz coil (rectangular setup)
Ever wondered how scientists trap and manipulate charged particles with precision? The secret lies in the anti-Helmholtz coil, a marvel of electromagnetic engineering that creates magnetic field gradients essential for groundbreaking experiments. Our Anti-Helmholtz Coil Simulator brings this complex phenomenon to your fingertips, allowing you to explore the fascinating world of magnetic field gradients. Play with the variables of the simulator, and observe how they affect the overall magnetic field. Dive in and start simulating now!
\[
B_{\mathrm{coil}}(z)
= \frac{\mu_0 N I}{\pi}\;
\frac{L\,H}{\sqrt{L^{2}+H^{2}+z^{2}}}
\left(
\frac{1}{L^{2}+z^{2}} + \frac{1}{H^{2}+z^{2}}
\right).
\]
and
\( B_{\rm AH}(z) = B_{\rm coil}(z – \frac{d}{2}) – B_{\rm coil}(z + \frac{d}{2})\)
Mathematical description
The gradient of the magnetic field at the center along the axis (z-axis) is approximately given by
where:
- \(B_{\mathrm{coil}}(z)\) is the magnetic field along the axis of the coils.
- \( B_{AH}(z) \) is the magnetic field along the axis of the anti-Helmholtz configuration coils.
- \( 2L \) is the length of rectangle.
- \( 2H \) is the width of rectangle.
- \( d \) is the distance between the two coils (separation)
- \( N \) is the number of turns in each coil
- \( I \) is the current through the coils
- \( \mu_0 \) is the magnetic permeability of free space, \( \mu_0 = 4 \pi \times 10^{-7} \, \text{T·m/A} \)
Tutorial video
Anti-Helmholtz Simulation
Take a quick spin through our simulator!
Simulator
Experiment with the controls, change variables, and see how they affect the overall magnetic field in a rectangular coil configuration.
Interactive Physics Simulator – Anti-Helmholtz Coils
🌟 You May Also Like
Suggested experiments and activities based on your progress...
FAQs on Anti-Helmholtz coil
Qus 1. What is an Anti-Helmholtz coil used for?
Anti-Helmholtz coils are used to create magnetic field gradients, which are essential for trapping and manipulating charged particles in applications like atomic physics and magnetic confinement in plasma research.
Qus 2. How does an Anti-Helmholtz coil work?
An Anti-Helmholtz coil consists of two identical coils placed apart with currents flowing in opposite directions. This configuration generates a magnetic field that decreases linearly between the coils, creating a gradient useful for particle trapping and manipulation.
Qus 3. What are the differences between Helmholtz and Anti-Helmholtz coils?
Helmholtz coils generate a uniform magnetic field with currents flowing in the same direction, while Anti-Helmholtz coils produce a gradient magnetic field with currents flowing in opposite directions. Helmholtz coils are ideal for consistent magnetic fields, while Anti-Helmholtz coils are suited for field gradients.
Qus 4. In anti-helmholtz coils do we need to keep ths distance between the coils equal to coil radius?
No, in an anti-Helmholtz coil setup, the distance between the coils should not match the coil radius. Instead, the coils are positioned as close together as possible while preserving the desired geometry. The defining characteristic of an anti-Helmholtz coil is that the currents in the two coils flow in opposite directions, generating a magnetic field that largely cancels out in the central region between the coils.
Qus 5. How does an Anti-Helmholtz coil produce magnetic field gradient?
Think of the “Anti-Helmholtz coil” setup as a combination of two solenoids. These two solenoids are placed closed to each other with current flowing in opposite directions in them. Both the solenoids will generate respective magnetic fields and these fields will interact to give us a magnetic field gradient.
- Magnetic Field Generation: Each coil generates its own magnetic field when an electric current passes through it. Due to the opposite direction of currents, the magnetic fields produced by the two coils also have opposite orientations.
- Field Interaction: The interaction of these oppositely oriented fields creates a non-uniform magnetic field. In the center region between the two coils, the magnetic fields from each coil cancel out along the axis between them, resulting in a decreasing magnetic field strength as you move from the center outward.
- Linear Variation: The result is a magnetic field gradient, meaning the magnetic field strength changes linearly with distance in the central region between the coils. The gradient is highest near the center and decreases as you move away from it
Qus 6. How's rectangular anti-Helmholtz coil diferent than circular anti-helmholtz coil set up?
Rectangular anti-Helmholtz coils behave the same way as circular ones in concept, but the formulas differ. For circular coils we integrate the contribution of the continuous loop; for rectangular coils we sum the contributions of the four straight segments. Because the segment geometry is different, the on-axis integrals change and the resulting field expressions are not identical.
1) Start from the Biot–Savart law for a current element:
\[d\mathbf{B}(\mathbf{r}) = \frac{\mu_0}{4\pi} I \frac{d\mathbf{l} \times (\mathbf{r}-\mathbf{r}’)}{|\mathbf{r}-\mathbf{r}’|^3}.\]
For a rectangular loop in the x-y plane, centered at the origin, the z-axis field at (0,0,z)is obtained by summing the z-components of the contributions from the four sides.The contribution of a side parallel to the y-axis at x = +L (y from -H to +H) evaluates to an elementary integral which can be done in closed form.
2) Now axial field of a single rectangular loop (half-dimensions L,H)
\[
B_{\mathrm{coil}}(z)
= \frac{\mu_0 N I}{\pi}\;
\frac{L\,H}{\sqrt{L^{2}+H^{2}+z^{2}}}
\left(
\frac{1}{L^{2}+z^{2}} + \frac{1}{H^{2}+z^{2}}
\right).
\]
Explanation: This expression is obtained by integrating the Biot–Savart contribution of each straight segment and summing all four segments (two vertical sides at x=±L and two horizontal sides at y=±H). – L = l/2 and H = b/2.
3) Anti-Helmholtz pair (two identical coils at z = ±d/2 with opposite currents)
The axial field of an Anti–Helmholtz pair (coils centered at z=+d/2 and z=-d/2, currents +I and -I)
is obtained by superposition:
\[
B_{\mathrm{AH}}(z)
= B_{\mathrm{coil}}\!\left(z-\frac{d}{2}\right)
– B_{\mathrm{coil}}\!\left(z+\frac{d}{2}\right).
\]
4) Field at the midplane z = 0 (cancellation)
At the midplane z=0 the fields from the two coils cancel (because currents are opposite and geometry symmetric):
\[
B_{\mathrm{AH}}(0)
= B_{\mathrm{coil}}\!\left(-\frac{d}{2}\right)
– B_{\mathrm{coil}}\!\left(+\frac{d}{2}\right)
= 0.
\]
(Zero field at center is the characteristic of an anti-Helmholtz pair.)
5) Axial gradient at the midplane
The axial gradient evaluated at the midplane z=0 is
\[
\left.\frac{dB_{\mathrm{AH}}}{dz}\right|_{z=0}
= 2 \left.\frac{dB_{\mathrm{coil}}}{dz}\right|_{z=\frac{d}{2}}.
\]
6) Explicit derivative dB_coil/dz (closed form)
Define for compactness D = L^{2}+H^{2}+z^{2}. Then differentiate the boxed B_coil(z).
A convenient form for the derivative is:
\[
\begin{aligned}
\frac{dB_{\text{coil}}}{dz}
&= \frac{\mu_0\,N\,I\,L\,H}{\pi}\; z \;\times\\[4pt]
&\quad\Bigg[
-\,\frac{1}{D^{3/2}}\left(\frac{1}{L^{2}+z^{2}}+\frac{1}{H^{2}+z^{2}}\right)
\;-\;\frac{2}{D^{1/2}}\left(\frac{1}{(L^{2}+z^{2})^{2}}+\frac{1}{(H^{2}+z^{2})^{2}}\right)
\Bigg].
\end{aligned}
\]
7) Anti-Helmholtz gradient at the center (explicit)
Therefore the Anti–Helmholtz axial gradient at z=0 is
\[
\frac{dB_{\mathrm{coil}}}{dz}
= \frac{\mu_0 N I L H}{\pi}\; z\;
\left[
-\,\frac{1}{D^{3/2}}\left(\frac{1}{L^{2}+z^{2}}+\frac{1}{H^{2}+z^{2}}\right)
-\,\frac{2}{D^{1/2}}\left(\frac{1}{(L^{2}+z^{2})^{2}}+\frac{1}{(H^{1}+z^{2})^{2}}\right)
\right],
\]
where in the right-hand side you must substitute \(z=\dfrac{d}{2}\) and \(D=L^{2}+H^{2}+z^{2}\).
\[
\begin{aligned}
\mu_0 & : \text{permeability of free space } (4\pi \times 10^{-7}\,\text{H/m}) \\[6pt]
N & : \text{number of turns in each coil} \\[6pt]
I & : \text{current through each coil (A)} \\[6pt]
l & : \text{total length of the rectangular coil (x-direction)} \\[6pt]
b & : \text{total height of the rectangular coil (y-direction)} \\[6pt]
L &= \tfrac{l}{2} \; : \; \text{half-length of coil (semi-axis along x)} \\[6pt]
H &= \tfrac{b}{2} \; : \; \text{half-height of coil (semi-axis along y)} \\[6pt]
z & : \text{axial distance from the coil plane along the symmetry axis (z-axis)} \\[6pt]
d & : \text{center-to-center separation between the two coils in Anti-Helmholtz configuration} \\[6pt]
B_{\text{coil}}(z) & : \text{axial magnetic field at distance $z$ due to a single coil} \\[6pt]
B_{\rm AH}(z) & : \text{axial magnetic field due to the Anti-Helmholtz pair} \\[6pt]
\frac{dB_{\rm AH}}{dz} & : \text{axial magnetic field gradient of the Anti-Helmholtz pair}
\end{aligned}
\]
Qus 6. What are some of the real life applications of the magnetic gradient produced by the anti- Helmholtz coil setup?
Anti-Helmholtz coils create magnetic field gradients that trap and slow down atoms, reducing their kinetic energy and cooling them, which is essential for experiments in atomic physics and quantum mechanics.
Qus 7. How do Anti-Helmholtz coils aid in atomic cooling?
Common applications of Anti-Helmholtz coils include trapping and cooling atoms in atomic physics, magnetic confinement in plasma research, and precision measurements in scientific experiments.
- Particle Trapping: The magnetic gradient is especially useful for trapping and controlling the motion of charged particles or neutral atoms. It is commonly used in atomic physics experiments, such as in magneto-optical traps (MOTs) for cooling and trapping atoms.
- Preparation of qubits: The MOTs are used to trap ions and atoms. Once atoms are trapped, we can use lasers to control their quantum states—essentially flipping them between “0” and “1” (or combinations of both, which is unique to quantum computing). These atoms then become qubits, the basic building blocks of quantum computers.
- Magnetic Confinement: In plasma research, the magnetic field gradient helps in confining plasma, an essential aspect of fusion research.
Qus 8. What materials are Anti-Helmholtz coils typically made of?
Anti-Helmholtz coils are typically made of copper wire wound on a non-magnetic frame, chosen for its excellent electrical conductivity, ensuring efficient current flow and effective magnetic field generation.