Lorentz force simulator

Explore how magnetic fields interact with moving charged particles and visualize the resulting forces using our interactive simulator.

Lorentz force

Ever wondered how charged particles dance in magnetic fields or how electromagnetism powers countless technologies around us? It’s all thanks to a fundamental phenomenon known as the Lorentz force. Our “Lorentz force simulator” will bring this concept to life, allowing you to visualize the invisible forces at play. Experiment with the controls, change variables, and see how they affect the trajectory of charged particles. Clarify your doubts and deepen your understanding. Dive in and start simulating now!

$ \vec{F} = q(\vec{v} \times \vec{B})
$

Mathematical description

The Lorentz force (F) is the force experienced by a charged particle moving through electric and magnetic fields (B), acting perpendicular to both its velocity (v) and the magnetic field.

where:

$ F $ is Lorentz force
$ q $ is the charge on charge particle
$ v $ is the velocity of charge particle
$ B $ is the magnetic field

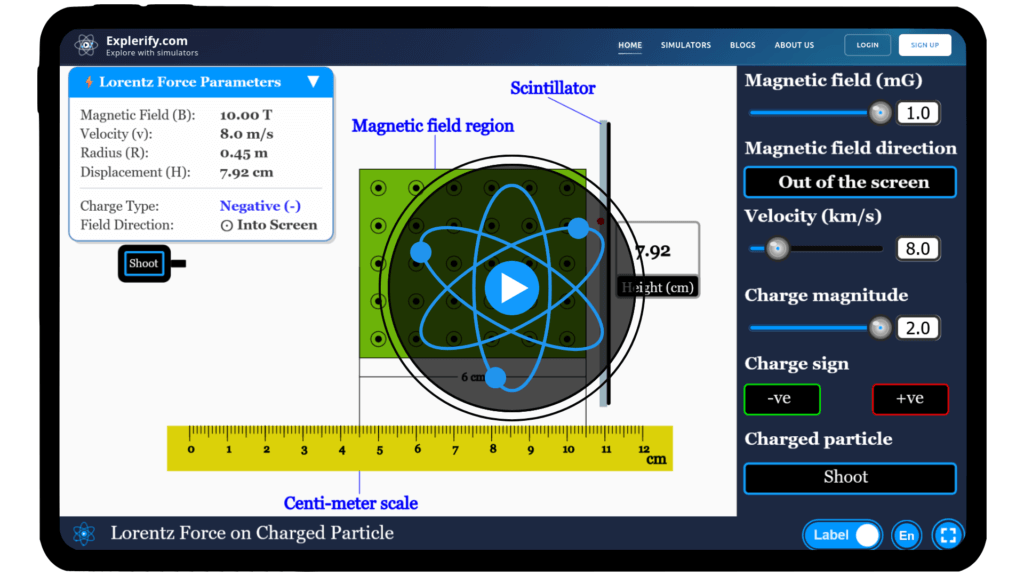
Simulator

Dive into the fundamentals of electromagnetism with our interactive Lorentz force simulator!

Share with your friends

FAQs on Lorentz Force

Qus 1. What is Lorentz force?

Lorentz force is the force that is experienced by a moving charged particle in a magnetic field. The charge particle experiences a force perpendicular to both its velocity and the magnetic field, causing it to move in a circular or helical path.

Qus 2. How is the direction of the force on a moving charge determined in a magnetic field?

The direction of the force on a moving charge in a magnetic field is determined by the right-hand rule. Point your thumb in the direction of the velocity, your fingers in the direction of the magnetic field, and your palm will point in the direction of the force for a positive charge (opposite for a negative charge).

Qus 3. What is the formula for the force on a moving charge in a magnetic field?

The formula for the force $\mathbf{F}$ on a moving charge $q$ in a magnetic field $\mathbf{B}$ is $\mathbf{F} = q(\mathbf{v} \times \mathbf{B})$ , where $\mathbf{v}$ is the velocity of the charge and $\times$ denotes the cross product.

Qus 4. Why does a charged particle move in a circular path in a magnetic field?

A charged particle moves in a circular path in a magnetic field because the magnetic force acts as a centripetal force, constantly changing the direction of the particle’s velocity while maintaining a perpendicular angle, resulting in circular motion.

Qus 5. How does the speed of a charged particle affect its motion in a magnetic field?

The speed of a charged particle affects the radius of its circular path in a magnetic field. A higher speed results in a larger radius, while the frequency of rotation (cyclotron frequency) remains constant.

The radius $r$ of the path of a charged particle in a magnetic field is given by $r = \frac{mv}{qB}$ , where $m$ is the mass, $v$ is the velocity, $q$ is the charge, and $B$ is the magnetic field strength.

Qus 6. How does a magnetic field affect the kinetic energy of a moving charge?

A magnetic field does not change the kinetic energy of a moving charge because the force is perpendicular to the motion, causing only a change in direction, not in speed or kinetic energy. Hence the magnetic field does no work on the moving charge leading to no change in kinetic energy

Qus 7. What is the significance of the Lorentz force in electromagnetism?

The Lorentz force is fundamental in electromagnetism, describing how charged particles interact with electric and magnetic fields. Some of the applications of Lorentz force are:

cyclotrons and synchrotrons for particle acceleration
magnetic confinement in fusion reactors
mass spectrometry for analyzing substances based on their charge-to-mass ratio.
Van Allen Belts- Charged particles spiral along Earth’s magnetic field lines due to the Lorentz force, forming radiation belts which protect Earth from harmful solar radiation.

Qus 8. What is the difference between the motion of charged particles in electric and magnetic fields?

In an electric field, charged particles accelerate in the direction of the field, gaining kinetic energy. In a magnetic field, particles move in circular or helical paths without a change in speed but with a change in direction.