Searle's apparatus simulator

Explore elasticity interactively: Dive into the physics of elasticity and discover how Young's modulus of a material is experimentally determined.

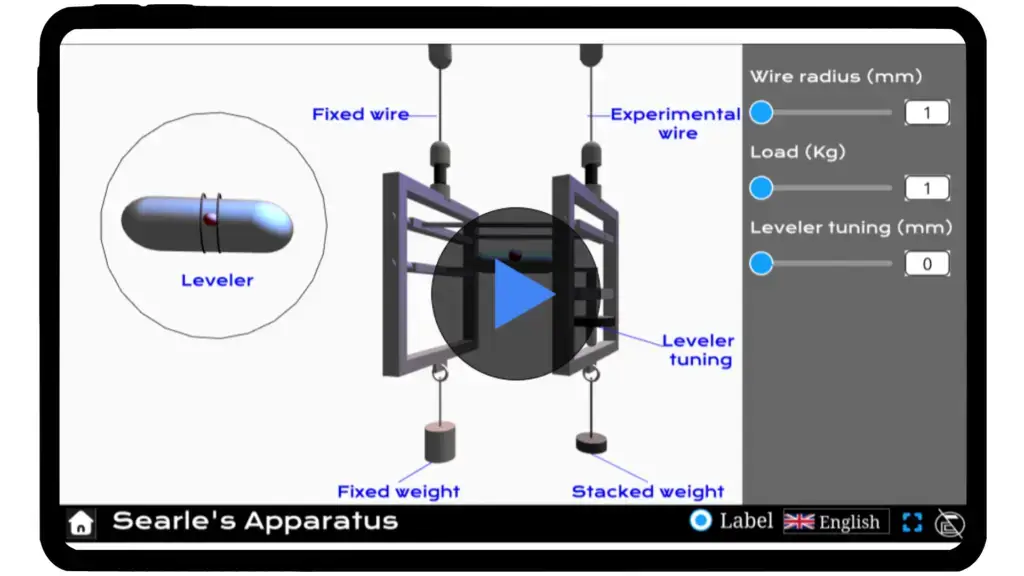
Searle's apparatus

Elasticity plays a key role in materials, from everyday objects to advanced engineering. Ever wondered how load affects extension? Step into the world of material properties with our interactive Searle’s Apparatus Simulator. Adjust the load, experiment with different materials, and see how stress and strain interact in real time. Uncover the principles of elasticity—start your exploration today!

\( Y = \frac{4 \cdot M \cdot g \cdot L}{\pi \cdot d^4 \cdot \Delta L}
\)

Mathematical description

where:

\( Y \) is the Young’s Modulus of the material
\( M \) is the mass applied to the wire (load)
\( g \) is the acceleration due to gravity (9.8 m/s²)
\( L \) is the original length of the wire
\( d \) is the diameter of the wire
\( \Delta L \) is the extension of the wire due to the applied load

Tutorial video

Take a quick spin through our simulator!

Simulator

Discover how Young’s Modulus is calculated with our interactive Searle’s Apparatus Simulator!
Adjust the wire radius and applied load to explore the precise tuning required to keep the ball perfectly leveled in the spirit level.

Interactive Physics Simulator – Searle's Apparatus

Share with your friends

Compact User Progress Tracker

Explore Searle's Apparatus -

One Question at a time!

Qus 1. What is Searle's apparatus used for?

Searle’s apparatus is used to measure the Young’s modulus of elasticity of a material. It helps determine how a material deforms under stress, making it useful in physics experiments and material science studies. Young’s modulus is mathematically defined as the ratio of stress (force per unit area) applied to an object to the resulting axial strain (deformation per unit length) it produces.

Qus 2. How does Searle's apparatus work?

Searle’s apparatus works by suspending a wire of the material under test. A micrometer screw gauge measures the extension in the wire when a known weight is added. The Young’s modulus is calculated using the formula: \( Y = \frac{F \cdot L}{A \cdot \Delta L}
\)
where \( F \) is the applied force, \( L \) is the length of wire, \( A \) is the cross-section area, and \( \Delta L \) is the extension.

Qus 3. Why is Young's modulus important in Searle's apparatus experiments?

Young’s modulus quantifies a material’s ability to resist deformation under stress. Searle’s apparatus provides a practical way to calculate this property, helping engineers and scientists select suitable materials for construction, machinery, and other applications.

Qus 4. What are the main components of Searle's apparatus?

Searle’s apparatus typically includes:

Two suspended wires (one for testing and one for reference).
A weight hanger to apply load.
A micrometer screw gauge to measure extension.
A spirit level for precise alignment.

Qus 5. What are the precautions to take while using Searle's apparatus?

To ensure accurate results:

Use a thin, uniform wire of consistent material.
Align the apparatus perfectly with the spirit level.
Avoid applying excessive load to prevent wire breakage.
Take multiple readings to minimize errors.

Qus 6. What are the limitations of Searle's apparatus?

One wire acts as the test wire, and the other serves as a reference. The reference wire ensures that any environmental factors (like temperature changes or vibrations) affecting both wires equally do not skew the experimental results.

Qus 7. What materials can be tested with Searle's apparatus?

Searle’s apparatus can test materials like metals (e.g., steel, copper) and alloys. The material must be ductile enough to elongate without breaking under stress.

Qus 8. Why experimental values obtained by Searle's apparatus often differ from theoretical values?

In most cases, the experimental value of Young’s modulus differs from the theoretical value found in textbooks. This difference arises due to several practical limitations and sources of error, such as:

Temperature Variations: Even a slight change in room temperature can alter the wire’s length and elasticity, affecting the readings.
Measurement Errors: Parallax errors while reading the micrometer screw gauge or scale can lead to incorrect elongation values.
Imperfect Alignment: If the wire is not perfectly vertical or the load is unevenly applied, extra bending stress is introduced.
Initial Slack or Kinks: Any slack in the wire before adding the load causes non-uniform extension during the first few readings.
Elastic Fatigue: Repeated loading and unloading can cause the wire to lose some elasticity, leading to lower measured values.
Neglecting the Weight of the Wire: The wire’s own weight exerts a small but measurable tension, which is often ignored in theoretical calculations.

Qus 8. Explain why temperature plays such a dominant role in affecting the Searle's apparatus results?

Temperature changes alter both the physical length and the elastic behavior of the wire, making them one of the most critical sources of error in Searle’s apparatus.
Even a small increase of 1–2°C can cause a noticeable change in the wire’s length, especially since we’re measuring extensions in the order of millimeters or micrometers. This expansion can falsely appear as extra elongation due to load — leading to an underestimation of Young’s modulus.
At the same time, temperature also affects the interatomic forces in the metal. Higher temperature means the atoms vibrate more, weakening the restoring forces that resist deformation. As a result, the wire becomes slightly more flexible, again reducing the apparent modulus of elasticity.

Qus 9. Why are two wires used in Searle's apparatus?

Qus 10. How does Searle’s apparatus ensure precise measurements?

The spirit level ensures proper alignment, while the micrometer screw gauge accurately measures minute extensions. The use of a reference wire helps eliminate errors due to environmental factors.

Qus 11. What are the practical applications of searle's apparatus

The applications of Searle’s apparatus extend to several practical areas:

Material Testing: Used in labs to compare the elasticity of different metals and alloys.
Engineering Design: Helps engineers select suitable materials for bridges, cables, and mechanical components where tensile strength and elasticity are critical.
Quality Control: Industries use the principle of Searle’s apparatus to test whether a wire or material batch meets mechanical standards.
Research Applications: Forms the basis for more advanced experiments involving strain gauges and material deformation analysis.

Searle's apparatus simulator

Explore elasticity interactively: Dive into the physics of elasticity and discover how Young's modulus of a material is experimentally determined.