Projectile motion simulator
Explore projectile motion interactively: discover the relationship between velocity, angle, and trajectory with our engaging simulator.
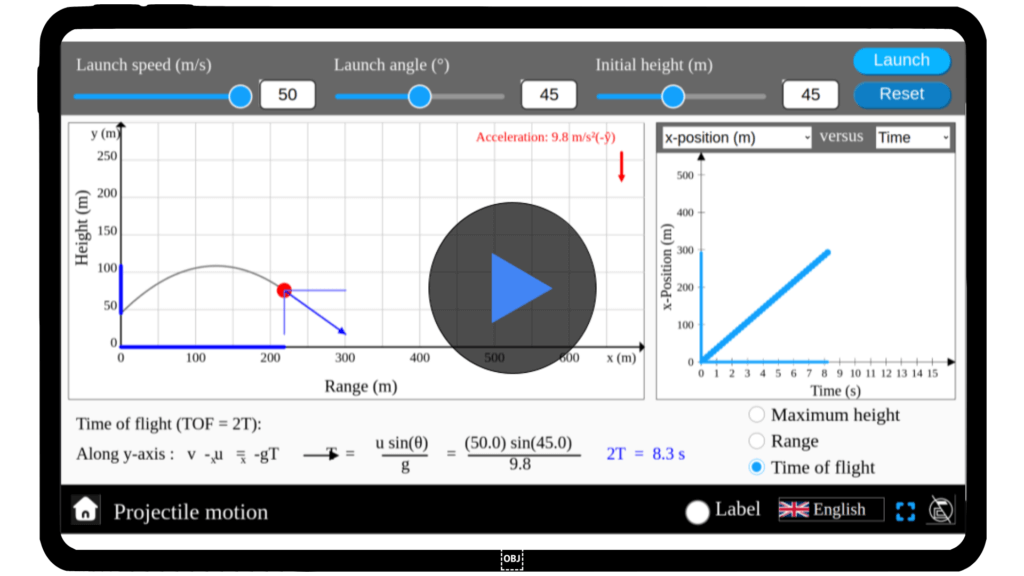
Projectile motion
Projectiles are a key part of motion, from sports to space exploration. But have you ever wondered how velocity, angle, and gravity influence a projectile’s path? Step into the world of projectile motion with our interactive simulator. Adjust launch angles, velocities, and observe how they affect range and height in real-time. Uncover the principles of motion—start your exploration today!
FAQs on Projectile motion
Qus 1. What is projectile motion?
Projectile motion refers to the motion of an object thrown into the air, moving under the influence of gravity while following a curved trajectory. It is a combination of horizontal motion and vertical free-fall motion.
Qus 2. What factors affect projectile motion?
Key factors include:
- Initial velocity (higher velocity increases range and height).
- Angle of projection (affects trajectory).
- Gravity (reduces range and height).
- Air resistance (not considered in ideal cases but reduces motion in real-life scenarios).
Qus 3. What is the formula for the range of a projectile?
The formula for the range is:
\begin{equation}
R = \frac{v^2 \sin(2\theta)}{g}
\end{equation}
where \(v\) is velocity, \(\theta\) is angle of projection and \(g\) is the acceleration due to gravity.
Qus 4. How do you calculate the time of flight in projectile motion?
The time of flight is given by:
\begin{equation}
T = \frac{2v \sin\theta}{g}
\end{equation}
where \(v\) is velocity, \(\theta\) is angle of projection and \(g\) is the acceleration due to gravity.
Qus 5. What is the maximum height of a projectile?
The maximum height is calculated using:
\begin{equation}
H = \frac{v^2 \sin^2 \theta}{2g}
\end{equation}
where \(v\) is velocity, \(\theta\) is angle of projection and \(g\) is the acceleration due to gravity.
Qus 6. What is the optimal angle for maximum range in projectile motion?
The optimal angle for achieving the maximum range is 45 degrees, assuming no air resistance. At this angle, the horizontal and vertical components of velocity are perfectly balanced.
Qus 7. How is projectile motion used in real life?
Projectile motion is applied in sports (e.g., basketball, football), military ballistics, designing fireworks, and engineering projects like bridges and dams that involve trajectories.
Qus 8. Can a projectile's range be greater than its height?
Yes, the range is usually much greater than the height unless the angle of projection is very steep. The ratio depends on the angle of projection and the initial velocity.
Qus 9. How does air resistance affect projectile motion?
Air resistance slows down the horizontal and vertical components of velocity, shortening the range and reducing the maximum height. Real-world projectiles always experience some air resistance. To understand the effect of air resistance in detail, refer to this article.
Qus 10. What is the difference between horizontal and vertical components of velocity in projectile motion?
- Horizontal velocity remains constant throughout the motion (ignoring air resistance).
- Vertical velocity changes due to gravity, decreasing as the projectile ascends and increasing as it descends.
Qus 11. What happens to a projectile at the top of its trajectory?
At the highest point, the vertical velocity becomes zero, while the horizontal velocity remains constant. The projectile is momentarily moving only horizontally at this point.
Qus 12. Why does a projectile follow a parabolic path?
The parabolic path is due to the combination of constant horizontal velocity and uniformly accelerated vertical motion caused by gravity. This creates a symmetrical curve.