Time period of pendulum simulator

Explore the motion of pendulums interactively: discover the relationship between length, gravity, and time period with our engaging simulator!

Time period of pendulum

Pendulums have fascinated scientists and engineers for centuries, from simple clocks to advanced physics experiments. But what governs their motion? Dive into the world of pendulum mechanics with our interactive simulator. Adjust the length, experiment with gravity, and observe how these factors influence the time period. Unravel the principles of harmonic motion and see physics in action — start your exploration today!

\( T = 2\pi \sqrt{\frac{L}{g}}
\)

Mathematical description

where:

\( T \) is the Time period (time for one complete oscillation)
\( L \) is the Length of the pendulum (distance from the pivot to the center of mass of the bob)
\( g \) is the Acceleration due to gravity

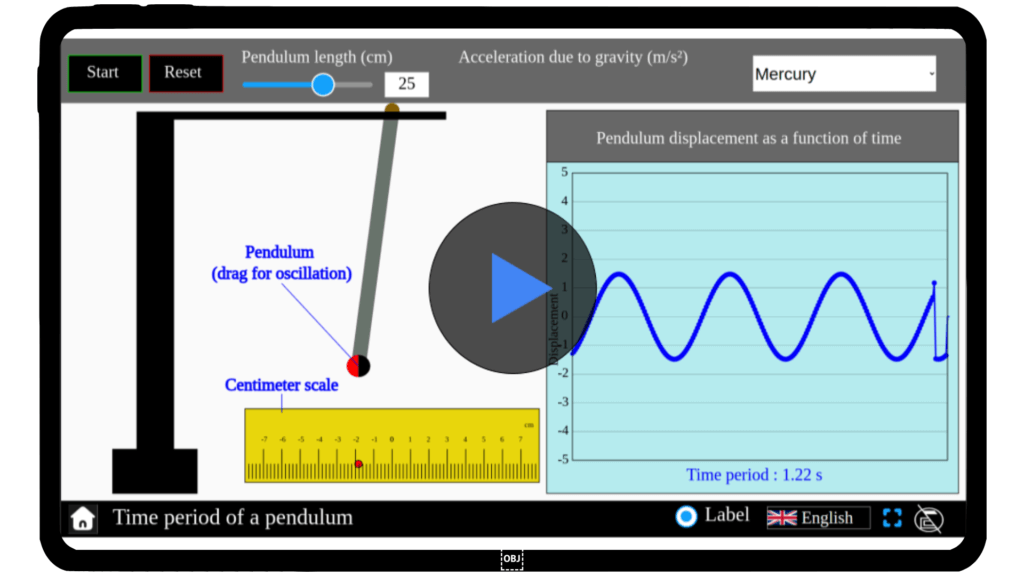
Simulator

Drag the bob of the pendulum and experiment with the parameters to observe how time period of pendulum gets affected.

Interactive Physics Simulator – Pendulum Time Period

Share with your friends

Compact User Progress Tracker

FAQs on Time Period of a Pendulum

Qus 1. What is the time period of a pendulum?

The time period of a pendulum is the time it takes to complete one full oscillation, moving from one extreme point to the other and back. It depends on the length of the pendulum and the acceleration due to gravity.

Qus 2. What factors affect the time period of a pendulum?

The time period is affected by:

Length of the pendulum (longer pendulums have longer periods).
Gravity (stronger gravity shortens the period).
It is not affected by the mass of the bob or the amplitude (for small oscillations).

Qus 3. Why doesn’t the mass of the bob affect the time period of a pendulum?

The mass of the bob influences both the gravitational force pulling it down and its resistance to motion (inertia) in exactly the same way. As a result, these effects cancel each other out, making the time period of a pendulum independent of the mass of its bob. This is a key demonstration of how gravitational and inertial mass are equivalent, as stated by Galileo and later formalized by Newton and Einstein.

Qus 4. Can the time period of a pendulum be used to measure gravity?

Yes, by rearranging the formula \( T = 2\pi \sqrt{\frac{L}{g}}
\) the value of g can be determined if the length of the pendulum and its time period are known. This method is often used in physics experiments.

Qus 5. What are real-life applications of the pendulum's time period?

The pendulum’s time period is used in:

Designing clocks (e.g., pendulum clocks).
Measuring gravity in scientific studies.
Teaching basic principles of physics and oscillatory motion.

Qus 6. What is a compound pendulum, and how is its time period different?

A compound pendulum consists of a rigid body swinging about a pivot point. Its time period depends on the distribution of mass and the distance between the pivot and the center of gravity, unlike a simple pendulum.

Qus 7. What happens to the time period of a pendulum if the length is halved?

If the length is halved, the time period is reduced by a factor of √2 (about 1.41). This is because the time period is proportional to the square root of the pendulum’s length.

Qus 8. How does temperature affect the time period of a pendulum?

Temperature changes can affect the length of a pendulum due to thermal expansion or contraction. For example, higher temperatures may increase the pendulum’s length, slightly increasing the time period.

Qus 9. Why is the pendulum considered a good example of simple harmonic motion?

For small oscillations, the restoring force acting on the pendulum is proportional to its displacement, a key characteristic of simple harmonic motion. This makes it an ideal example in physics.

Qus 10. What is the time period of a pendulum on the moon?

On the moon, the time period of a pendulum is longer because the gravitational acceleration (g) is weaker. Since \( T = 2\pi \sqrt{\frac{L}{g}}
\) , a lower value of g increases the time period.

Qus 11. What is the time period of a pendulum at the poles and the equator?

The time period is slightly shorter at the poles and longer at the equator because gravity is stronger at the poles and weaker at the equator.

Time period of pendulum simulator

Explore the motion of pendulums interactively: discover the relationship between length, gravity, and time period with our engaging simulator!